量子电路是量子计算机的核心部分，专用于执行量子计算任务。然而，与传统经典电路相比，量子电路面临技术挑战。在量子态制备环节，优化资源使用如减少量子门操作的数量、降低电路的复杂程度，是亟待解决的科学问题。这些因素决定量子算法的运行效率与可扩展性，还与减轻噪声干扰、提高量子态稳定性等相关，是推动量子计算走向实用化的前提。对此，科学家面临核心难题在于，为了制备特定的量子态，量子电路过浅会导致量子态制备不精确，过深则浪费资源。近日，中国科学院理论物理研究所团队等，提出了新的多体纠缠度量方法，通过分析多体纠缠熵与保真度的标度关系来优化量子电路，对上述难题给出了可实用化执行的解决方案。这一工作将量子纠缠、张量网络与量子计算实现结合起来，兼具重要理论价值与应用价值。基于张量网络，研究团队将矩阵乘积态作为参考流形，提出了全新的多体纠缠度量方法，引入了新的物理量——特定χ矩阵乘积纠缠（χ-MPE）。该方法的核心思想是：与传统几何纠缠仅考虑与乘积态流形的距离，以及难以有效反映多体纠缠的复杂结构不同，χ-MPE将目标量子状态与“最优”的张量网络状态进行比较。这里的“最优”是指目标状态与具有特定虚拟维度χ的MPS流形之间的最小保真距离。换言之，该方法不是直接衡量一个状态有多么“纠缠”，而是看它与“最接近的”、复杂度受限的量子状态有多远的距离。当χ=1 时，MPS就退化成最简单的“乘积态”，这时χ-MPE就变成了“几何纠缠”，它衡量的是与完全没有纠缠的状态间的距离。随χ的增大，流形覆盖的纠缠态范围逐步扩展，χ-MPE衡量的是与更复杂、但仍受限于特定复杂度纠缠态之间的距离。研究进一步将χ-MPE与变分量子电路的“深度”联系起来。在量子计算中，电路的深度直接关系到计算的效率、噪声敏感度及资源消耗规模。研究发现，χ-MPE与量子电路制备目标状态的保真度之间存在标度关系。研究通过理论推导和数值模拟，揭示了三种重要的标度行为——超线性标度、线性标度、亚线性标度。χ-MPE提供了新颖且可控的方式来量化多体纠缠，它与张量网络紧密结合，为理解复杂量子系统提供了新工具。分析χ-MPE与保真度的标度关系，可以直接判断当前变分量子电路的深度是否最优，从而指导量子算法的设计和优化，降低资源消耗，提高量子计算的效率和鲁棒性，成为量子电路优化的利器。同时，这种基于张量网络的方法可以推广到其他类型的张量网络结构，为评估更广泛的量子电路在制备各类张量网络状态时的最优性提供了可能。相关研究成果发表在《物理评论快报》（Physical Review Letters）上。研究工作得到科学技术部、国家自然科学基金委员会、中国科学院等的支持。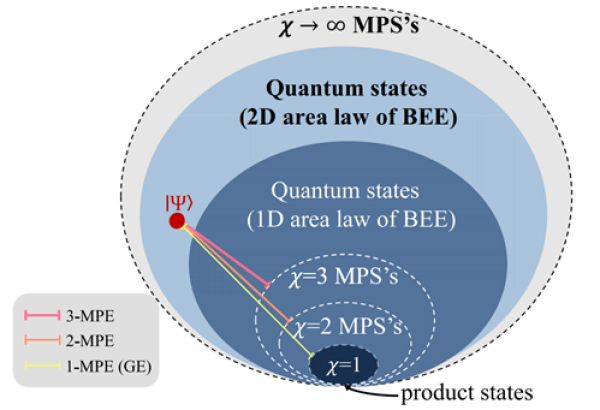论文链接量子电路优化研究获进展